Ensembling Methods Chinese Version
简介
在决策树章节中,我们讨论了如何在回归和分类任务中应用决策树,以及如何构建决策树。正如决策树章节中所述,决策树模型能力有限,过拟合问题难以解决,我们很难训练一个在一般情况下表现良好的决策树。因此,该章节中提出了使用决策树的集成算法。简而言之,多个训练模型的表现比单个模型的表现会更好。
我们有n个独立同分布的随机变量$X_i$,其中$0 \leq i \leq n$,并假设所有$X_i$有$Var(X_i) = \sigma^2$。那么,我可以得到$X_i$均值的方差为:
\[Var(\bar{X}) = Var(\frac{1}{n}\sum\limits_i X_i) = \frac{\sigma^2}{n}\]如果我们删除$X_i$独立的假设,则随机变量间是彼此相关的。
\[\begin{align} Var(\bar{X})&=Var(\frac{1}{n}\sum\limits_i X_i) \\ &= \frac{1}{n^2}\sum\limits_{i,j}Cov(X_i,X_j) \\ &= \frac{n\sigma^2}{n^2} + \frac{n(n-1)p\sigma^2}{n^2} \\ & = p\sigma^2 + \frac{1-p}{n}\sigma^2 \end{align}\]其中p是皮尔逊相关系数 $p_{X,Y} = \frac{Cov(X,Y)}{\sigma_x\sigma_y}$。我们知道 Cov(X,X) = Var(X)。
数学: 以下证明有助于理解上述步骤。
\[\begin{align} Var(\frac{1}{n}\sum\limits_i X_i) &= \frac{1}{n^2} Var(\sum\limits_i X_i) \\ &= \mathbb{E}[(\sum\limits_i X_i)^2] - (\mathbb{E}[\sum\limits_i X_i])^2 \\ &=\mathbb{E}[\sum\limits_{i,j}X_i X_j] - (\mathbb{E}[\sum\limits_i X_i])^2 \\ &=\sum\limits_{i,j}\mathbb{E}[X_iX_j]- (\mathbb{E}[\sum\limits_i X_i])^2 \\ &= \sum\limits_{i,j}\mathbb{E}[X_iX_j] - \sum\limits_{i,j}\mathbb{E}[X_i] \mathbb{E}[X_j] \\ &= \sum\limits_{i,j} \mathbb{E}[X_iX_j] - \mathbb{E}[X_i] \mathbb{E}[X_j] \\ &= \sum\limits_{i,j} Cov(X_i,X_j) \end{align}\]返回主题:现在,如果我们将每个随机变量视为一个训练模型的误差,我们可以通过以下方式减少此方差:
1, 增加随机变量(即模型数量)n的数量以式子后半部分变小
2,减少每个随机变量之间的相关性,使第一项变小,使其更靠近独立同分布状态
问题是,我们如何实现这些目标呢?在此章节中,我们将介绍Bagging和Boosting。
Bagging
Bootstrap
简单来讲,Bootstrap是一种重新采样技术,它可以用于改进数据的estimator。在该算法中,我们从数据的经验分布中不断采样,最后得到数据的统计值。
假设我们有一个经过训练的estimator E,这个estimator可以预测数据的中位数。我们想知道这个estimator估算的置信度有多高,以及它与真实数据的差异有多大。这里我们可以使用bootstrap来进行测评。在bootstrap算法中,我们可以:
1, Bootstrap样本$\mathbb{B}_1,\dots,\mathbb{B}_B$,其中$\mathbb{B}_b$,是通过从数据为n的数据集中有放回的抽取样本而生成的。
2, 得到每个Bootstrap $\mathbb{B}_b$的estimator为:
\[E_b = E(\mathbb{B}\_b)\]3, 计算E的均值与方差:
\[\mu_B = \frac{1}{B}\sum\limits_{n=1}^B E_b, \sigma_B^2 = \frac{1}{B}\sum\limits_{b=1}^B (E_b - \mu_B)^2\]这可以让我们了解estimator在估算数据中值时的表现如何。
Bagging
Bagging使用bootstrap的概念进行回归或分类,它代表着Bootstrap聚合。
算法如下:
对于$b=1,\dots,B$,
1, 从训练数据集中提取大小为n的bootstrap数据$\mathbb{B}_b$
2, 对bootstrap数据$\mathbb{B}_b$训练决策树分类器或决策树回归模型$f_b$。
要预测新数据点$x_0$,我们需要计算:
\[f(x_0) = \frac{1}{B} \sum\limits_{b=1}^B f_b(x_0)\]对于回归问题,我们只需要计算出所有分类器的预测平均值即可。对于分类任务,我们可以使用投票机制来获得最终结果。
假设在二元分类中,有一个输入特征$x\in \mathbb{R}^5$。如下所示,我们可以使用bootstrap算法来训练多个分类器:
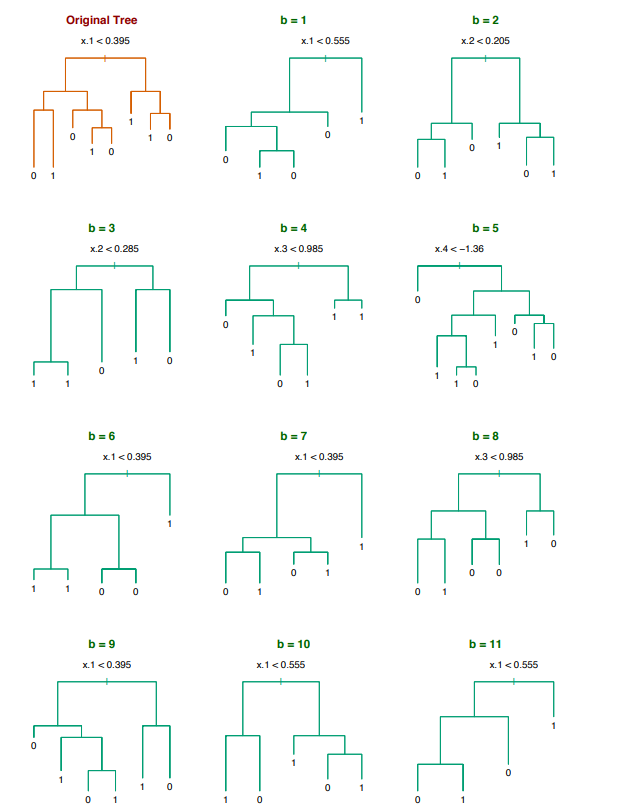
让我们回到等式:
\[Var(\bar{X}) = p\sigma^2 + \frac{1-p}{n}\sigma^2\]正如我们所讨论的,减少误差的一种方法是使每个训练模型上的相关性变小。 Bagging可以通过对不同的数据集训练,实现这一目标。我们无法否认的是,由于每个bootstrp从原始数据集中只获取部分训练样本,这可能会使偏差加大。然而事实证明,由此带来的误差的减少将大于偏差的增加。此外,我们可以通过引入更多模型(即增加M或者在等式中的n)不断减少误差。这并不会导致过拟合,因为$p$对M不敏感,所以整体误差只会减少。
以下两点需要强调:
1, 用bagging时,每个决策树并不需要做到完美,OK就差不多了。
2, Bagging在非线性数据中表现更好。
Out-of-bag estimation
在每个bootstrap中,我们只选择原始数据集的一部分。让我们假设我们均匀分布中对其进行有放回采样。随着数据集大小为$n\rightarrow \infty$,对于某一个样本,它未被选择的概率为:
\[\begin{align} \lim\limits_{n\rightarrow \infty} (1-\frac{1}{n})^n &= \lim\limits_{n\rightarrow \infty} \exp(n\log(1-\frac{1}{n})) \\ &\approx \exp(-n\frac{1}{n}) \\ &= \exp(-1) \end{align}\]这大约是三分之一,这意味着一个bootstrap中约有三分之一的原始数据未被选中进行训练。为了测试我们的bagging训练模型,对于第i个样本,我们可以用未经过该样本训练过的那些模型(大约M / 3模型)在此样本上进行预测。通过在整个数据集中执行此操作,我们可以获得out-of-bag(词如其名,bagging外的误差)误差估计。在$M\rightarrow\infty$的极端情况下,未对第i个样本进行训练的模型,对所有其他样本进行了训练,这个效果与交叉验证的留一法相同。
随机森林
不过Bagging也是存在缺点的。从bootstrap训练的决策树是彼此相关的,因为bootstrap之间是相关的。这是我们不想见到的,我们只希望减少相关性。这样的bagging将无法获得最佳性能。因此,有人就提出了随机森林,这种方法,修改虽小但却很有效。bagging是在所有维度上生长决策树,随机森林则是在随机选择的维度子集中生长决策树,详细为:
对 $b=1,\dots,B$,
1, 从训练数据集中提取大小为n的bootstrap$\mathbb{B}_b$
2, 对于每次训练,我们从d维度中随机选择m维($m \approx \sqrt(d)$)。对于每个bootstrap,我们有不同的维度m。
Boosting
我们现在知道了bagging是为了减少使用决策树时的方差,而Boosting则是为了减少偏差。在bagging中,我们生成bootstrap样本训练每个模型。在boosting中,我们在每次训练迭代后对bootstrap中的每个样本进行重新加权。如图所示:
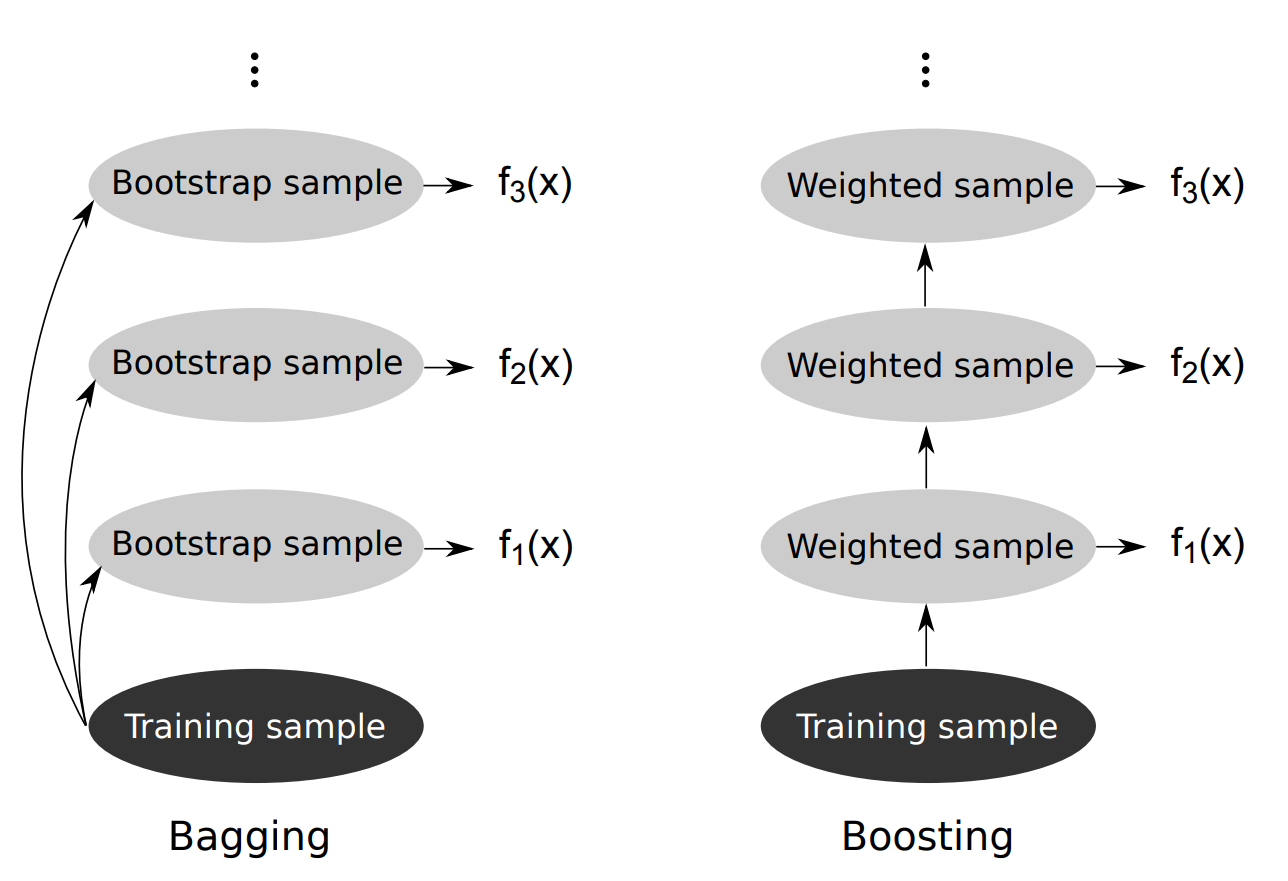
定义上讲,Adaboost为:
1, 初始化 $w_i \leftarrow \frac{1}{N}$ 其中 $i=1,2,\dots,n$ 并且这是一个二元分类。
2, 对 m=0 到 M:
根据分布$w_t(i)$对大小为n的bootstrap数据集$B_m$进行采样
将bootstrap $B_t$与模型$F_m$进行拟合
设 $\epsilon_m = \sum_{i=1}^n w_m(i) \mathbb{1}[y_i\neq F_m(x_i)] $ 并且 $\alpha_m = \frac{1}{2}\ln\frac{1-\epsilon_m}{\epsilon_m}$
缩放 $\bar{w}_{m+1}(i) = w_m(i)\exp(-\alpha_m y_i F_m(x_i))$ 并且归一化 $w_{m+1}(i) = \frac{\bar{w}_{m+1}(i)}{\sum_j \bar{w}_{m+1}(j)}$
3, 分类所遵循的规则为 $f_{boost}(x_0) = sign(\sum_{m=1}^M \alpha_m)$
在每次迭代中,错误分类的样本的权重不断增加。最终预测由加权误差决定。计算求和的结构准许我们增加建模能力,但由于每个训练模型都是相关的,也会导致高方差的出现。因此,增加M也会增加方差。
Boosting分析
值得一谈的是Boosting训练的准确性。这部分是纯粹理论,如果你愿意可以跳过它。
定理: 使用AdaBoost算法,如果$\epsilon_m$是分类器$f_m$的加权误差,则最终分类为$f_{boost}(x_0)=sign(\sum_{m=1}^M \alpha_m f_m(x_0))$。那么训练误差可以被限制:
\[\frac{1}{n}\sum\limits_{i=1}^n \mathbb{1}[y_i\neq f_{boost}(x_i)] \leq \exp(-2\sum\limits_{m=1}^M (\frac{1}{2}-\epsilon_m)^2)\]即使每个$\epsilon_m$都只比随机猜测好一些,当M较大时M模型的总和(在指数位置)将会是一个很大的负值。因此,它有一个较小的上限。
证明:
为了证明这一点,我们希望借助一个中间值。如果我们知道 a < b 并且 b < c, 那么我就能确定 a < c。
回想:
\[\bar{w}\_{m+1}(i) = w_m (i) \exp(-\alpha_m y_i F_m(x_i))\] \[w_{m+1}(i) = \frac{\bar{w}_{m+1}(i)}{\sum_j \bar{w}_{m+1}(j)}\]我们可以定义:
\[Z_m = \sum_j \bar{w}\_{m+1}(j)\]那么,我们可以将其改写:
\[w_{m+1}(i) = \frac{1}{Z_m} w_m(i)\exp(-\alpha_m y_i F_m(x_i))\]利用上面的等式进一步改写为:
\[\begin{align} w_{M+1}(i) &= w_1(i)\frac{\exp(-\alpha_1 y_i F_1(x_i))}{Z_1} \times \frac{\exp(-\alpha_2 y_i F_2(x_i))}{Z_2} \\ &\dots\times \frac{\exp(-\alpha_M y_i F_M(x_i))}{Z_M} \end{align}\]由于最开始的设定,所以我们知道 $w_1(i) = \frac{1}{n}$。 我们有:
\[w_{M+1}(i) = \frac{1}{n}\frac{\exp(-y_i\sum_{m=1}^M \alpha_m F_m(x_i))}{\prod_{m=1}^M Z_m} = \frac{1}{n}\frac{\exp(-y_i h_M(x_i))}{\prod_{m=1}^M Z_m}\]其中我们定义 $h_M(x) = \sum_{m=1}^M \alpha_m F_m(x)$。b为 $\prod_{m=1}^M Z_m$。 接下来我们可以将权重改写为:
\[w_{T+1}(i) \prod_{m=1}^M Z_m = \frac{1}{n} \exp(-y_i h_M(x_i))\]然后,我们将训练误差带回。注意,对于任何 $z_1 <0< z_2$,$0 < \exp(z_1), 1<\exp(z_2)$。所以:
\[\begin{align} \frac{1}{n}\sum\limits_{i=1}^n \mathbb{1}[y_i\neq f_{boost}] &\leq \frac{1}{n}\sum\limits_{i=1}^n \exp(-y_i h_M(x_i)) \\ &= \sum\limits_{i=1}^n w_{M+1}(i)\prod_{m=1}^M Z_m = \prod_{m=1}^M Z_m \end{align}\]我们证明了,训练误差小于等于中间值“b”。接下来我们单独处理$Z_m$:
\[\begin{align} Z_m &= \sum\limits_{i=1}^n w_m(i)\exp(-y_i\alpha_m F_m(x_i)) \\ &= \sum\limits_{i:y_i=F_m(x_i)} \exp(-\alpha_m w_m(i) + \sum\limits_{i:y_i\neq F_m(x_i)} \exp(\alpha_m)w_m(i) \\ &= \exp(-\alpha_m)(1 - \epsilon_m) + \exp(\alpha_m)\epsilon_m \end{align}\]其中 $\epsilon_m = \sum_{i:y_i\neq F_m(x_i)} w_m(i)$。如果我们对于$\alpha_m$,使$Z_m$最小化,我们可以得到:
\[\alpha_m = \frac{1}{2}\ln (\frac{1 - \epsilon_m}{\epsilon_m})\]这正是我们在最开始时设定的。
我们可以将其带回并找出:
\[Z_m = 2\sqrt{\epsilon_m(1-\epsilon_m)} = \sqrt{1 - 4(\frac{1}{2} - \epsilon_m)^2}\]我们知道 $1 - x \leq \exp(-x)$,所以我们可以说:
$$Z_m = (1 - 4(\frac{1}{2} - \epsilon_m)^2)^{\frac{1}{2}} \leq (\exp(-4(\frac{1}{2} - \epsilon_m)^2))^{\frac{1}{2}} = \exp(-2(\frac{1}{2} - \epsilon_m)^2)
对于所有$Z_m$,我们可以有:
\[\prod_{m=1}^M Z_m \leq \exp(-2\sum_{m=1}^M (\frac{1}{2}-\epsilon_m)^2)\]前项逐步叠加模型
在讨论新的boosting算法之前,我们值得研究一下一般的集成框架。它被称为前项逐步叠加模型。详细来讲:
输入: 提供标签的训练数据 $(x_1,y_1),\dot,(x_N,y_N)$
输出: 集成分类器 f(x)
1, 初始化 $f_0(x) = 0$
2, 对于 m=1 到 M:
计算 $(\beta_m,\gamma_m) = \arg\min_{\beta,\gamma}\sum_{i=1}^N L(y_i,f_{m-1}(x_i) + \beta G(x_i;\gamma))$
设 $f_m(x) = f_{m-1}(x) + \beta_m G(x;\gamma_m)$
3, 输出 $f(x) = f_m(x)$
在每次迭代中,我们修正之前步骤中所有训练模型的权重和参数。G(x)是一个弱分类器,它的参数为$\gamma$。现在证明Adaboost是一种在二分类和指数损失中的特殊情况:
\[L(y,\bar{y}) = \exp(-y\bar{y})\]此外,我们还可以证明,如果我们代入平方亏损(squared loss),那么:
\[L=\sum\limits_{i=1}^N (y_i-(f_{m-1}(x_i) + G(x_i)))^2 = ((y_i-f_{m-1}(x_i)) - G(x_i))^2\]这意味着在这个推导中的平方损失的效果等于在对每一个残差 $(y_i-f_{m-1}(x_i))$拟合一个分类器。这只是对逐步叠加学习的一个简短介绍,如果你想了解更多相关知识,你应该去查阅一下课本等相关书籍。
梯度提升
Boosting的应用领域很广泛,它也是逐步叠加建模的一种。其核心思想是,在每次迭代后,我们都会得到一个弱分类器。也就是说,我们只需要每个分类器的分类效果稍强于随机猜测即可。在最后,我们可以汇集所有弱分类器,形成一个能力较强的分类器。在Adaboost中,对于每次迭代,我们希望新模型专注于重新加权过的数据样本。对于梯度提升,最重要的是我们希望新模型专注于有偏差预测的梯度。
步骤为:
1, 初始化 $f_0(x) = c$
2, 在第i次迭代, 对于样本 $j=1,\dots,N$, 计算:
\[g_{ij} = \frac{\partial L(y_i,f_{i-1}(x_i))}{\partial f_{i-1}(x_i)}\]现在, 在第i次迭代中,我们有 $(x_1,g_{1i}),\dots,(x_N,g_{Ni})$
3, 在第i次迭代的,用$(x_1,g_{1i}),\dots,(x_N,g_{Ni})$拟合新的决策树或回归树:
\[\gamma_i = \arg\min_{\gamma}\sum\limits_{j=1}^N (g_j-G(x_j;\gamma))^2\]4, 设
\[f_i(x) = f_{i+1}(x) + G(x;\gamma_i)\]我们可以通过M次迭代来获得$f_M(X)$,这就是最终的模型了。
同样,这只是对梯度Boosting的简短介绍,更多内容请翻阅教科书。下面两个链接非常有用:
