Generative Learning Algorithm in Chinese

Please note this post is a study note translated to Chinese by me. Click here to see the original English version in Wei’s homepage.

请注意: 本文是我翻译的一份学习资料，英文原版请点击Wei的学习笔记。

---

生成学习算法

1 判别模型

判别模型是一种对观测数据进行直接分类的模型，常见的模型有逻辑回归和感知机学习算法等。此模型仅对数据进行分类，并不能具象化或者量化数据本身的分布状态，因此也无法根据分类生成可观测的图像。

定义上，判别模型通过构建条件概率分布p(y|x;θ)预测y，即在特征x出现的情况下标记y出现的概率。此处p可以是逻辑回归模型。

2 生成模型

与判别模型不同，生成模型首先了解数据本身分布情况，并进一步根据输入x，给出预测分类y的概率。该模型有着研究数据分布形态的概念，可以根据历史数据生成新的可观测图像。

而贝叶斯分类就是一个典型的例子。在这个例子中，我们首先有一个先验分类。这个先验的分布其实就是我们对数据分布的一个假设（如高斯分布，二项分布或多项分布），我们假设我们选择的模型可以正确解释数据集中的隐含信息。从数据集中，我们可以知道哪些参数最适合我们选择的模型。在这个已计算出先验概率的模型中，我们可以使用贝叶斯公式来进一步计算每个类的概率，然后挑出较大的概率供我们使用。与此同时，给定任意一个先验概率分布，我们可以根据这个分布生成新的样本y，进而基于所选择的先验生成新的特征x（比如，基于一个患癌症的先验概率与分布，我们可以生成新的患病者特征x）。这就是所谓的生成过程。

3 高斯判别分析

高斯判别分析（GDA）是一个生成模型，其中p(x|y)是多元高斯正态分布。

3.1 多元高斯正态分布

在多元正态分布中，一个随机变量是一个$R^n$空间中的矢量值，其中n代表维度数。因此，多元高斯的均值向量 μ∈$R^n$，协方差矩阵Σ∈$R^n$ ，其中Σ是对称的半正定矩阵。其概率密度函数为：

\[p(x;\mu,\Sigma) = \frac{1}{(2\pi)^{n/2}\lvert \Sigma\rvert^{1/2}}\exp\bigg(-\frac{1}{2}(x - \mu)^T\Sigma^{-1}(x - \mu)\bigg)\]

如上所述，μ代表期望值。

随机向量Z（或者说，向量化的随机变量Z）的协方差为：

\[\begin{align} Cov(Z) &= E[(Z-E[Z])(Z-E[Z])^T] \\ &= E[ZZ^T - 2ZE[Z]^T + E[Z]E[Z]^T]\\ &= E[ZZ^T] - 2E[Z]E[Z]^T + E[Z]E[Z]^T\\ &=E[ZZ^T] - E[Z]E[Z]^T \end{align}\]

下图显示了几个密度函数，它们的均值均为零，但协方差不同：

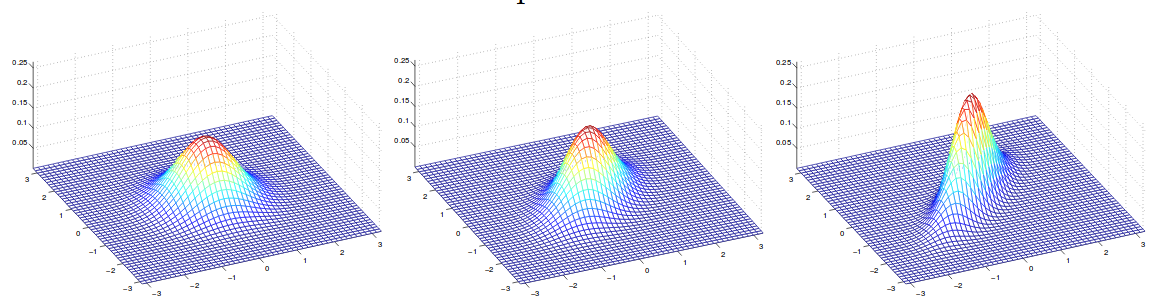
上图的协方差为（从左到右）：

\[\Sigma = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}; \Sigma = \begin{bmatrix} 1 & 0.5 \\ 0.5 & 1 \end{bmatrix}; \Sigma = \begin{bmatrix} 1 & 0.8 \\ 0.8 & 1 \end{bmatrix}\]

4 高斯判别分析和逻辑回归

4.1 高斯判别分析

我们再来谈谈二分类问题，我们可以用多元高斯模型对p(x|y)进行建模。 总的来讲，我们有：

\[y \sim Bernoulli(\phi)\] \[x\lvert y=0 \sim \mathcal{N}(\mu_0,\Sigma)\] \[x\lvert y=1 \sim \mathcal{N}(\mu_1,\Sigma)\]

在这里面，我们想要找出的参数φ，μ₀，μ₁，和Σ。 请注意，虽然每个类的均值不同，但它们的协方差相同。

这里有人会问，那为什么它是一个生成模型呢？简而言之，我们首先有一个类，也有这个类的y的先验概率分布，并且知道这个类的分布类型是伯努利分布。那么生成过程就是（1）从伯努利分布的类中抽样。 （2）基于类标签，我们从相应的分布中抽取x。这便是一个生成过程。

所以，该数据的对数似然函数值为：

\[\begin{align} \ell(\phi,\mu_0,\mu_1,\Sigma) &= \log \prod_{i=1}^m p(x^{(i)}, y^{(i)};\phi,\mu_0,\mu_1,\Sigma) \\ &= \log \prod_{i=1}^m p(x^{(i)}\lvert y^{(i)};\mu_0,\mu_1,\Sigma) p(y^{(i)};\phi)\\ &= \sum\limits_{i=1}^m \log p(x^{(i)}\lvert y^{(i)};\mu_0,\mu_1,\Sigma) p(y^{(i)};\phi) \end{align}\]

在上面的等式中，我们插入每个分布，但不指明具体这个分布是哪个类，我们仅将它们抽象为k。我们可以得到：

\[\begin{align} \ell(\phi,\mu_k,\Sigma) &= \sum\limits_{i=1}^m \log p(x^{(i)}\lvert y^{(i)};\mu_k,\Sigma) p(y^{(i)};\phi)\\ &= \sum\limits_{i=1}^m \bigg[-\frac{n}{2}\log 2\pi-\frac{1}{2}\log\lvert\Sigma\rvert \\ &-\frac{1}{2}(x^i-\mu_k)^T\Sigma^{-1}(x^i-\mu_k)\\ & + y^i\log\phi+(1-y^i)\log(1-\phi)\bigg]\\ \end{align}\]

现在，我们需要对每个参数进行取导，然后将它们设为零并找到 argmax（函数值最大时对应的输入值x）。 一些可能对推导有用的公式列举如下：

\(\frac{\partial x^TAx}{\partial x} = 2x^TA\) iff A is symmetric and independent of x

证明： 矩阵A是对称矩阵，所以 A= A^T并假设空间维度为n。

\[\begin{align} \frac{\partial x^TAx}{\partial x} &= \begin{bmatrix} \frac{\partial x^TAx}{\partial x_{1}} \\ \frac{\partial x^TAx}{\partial x_{2}} \\ \vdots \\ \frac{\partial x^TAx}{\partial x_{n}}\end{bmatrix} \\ &= \begin{bmatrix} \frac{\partial \sum\limits_{i=1}^n\sum\limits_{j=1}^n x_iA_{ij}x_j }{\partial x_{1}} \\ \frac{\partial \sum\limits_{i=1}^n\sum\limits_{j=1}^n x_iA_{ij}x_j}{\partial x_{2}} \\ \vdots \\ \frac{\partial \sum\limits_{i=1}^n\sum\limits_{j=1}^n x_iA_{ij}x_j}{\partial x_{n}} \end{bmatrix} \\ &= \begin{bmatrix} \frac{\partial \sum\limits_{i=1}^n A_{i1}x_i +\sum\limits_{j=1}^n A_{1j}x_j }{\partial x_{1}} \\ \frac{\partial \sum\limits_{i=1}^n A_{i2}x_i +\sum\limits_{j=1}^n A_{2j}x_j}{\partial x_{2}} \\ \vdots \\ \frac{\partial \sum\limits_{i=1}^n A_{in}x_i +\sum\limits_{j=1}^n A_{nj}x_j}{\partial x_{n}} \end{bmatrix} \\ &= (A + A^T)x \\ &= 2x^TA \blacksquare \end{align}\] \[\frac{\partial \log\lvert X\rvert}{\partial X} = X^{-T}\]

雅可比公式：

\[\frac{\partial \lvert X\rvert}{X_{ij}} = adj^T(X)_{ij}\]

证明：

\[\begin{align} \frac{\partial \log\lvert X\rvert}{\partial X}&=\frac{1}{\lvert X\rvert} \frac{\partial \lvert X\rvert}{\partial X} \\ &= \frac{1}{\lvert X\rvert} * adj^T (X)_{ij} \\ &= \frac{1}{\lvert X^T\rvert} * adj^T (X)_{ij} \\ &= X^{-T} \blacksquare \end{align}\] \[\frac{\partial a^TX^{-1}b}{\partial X} = -X^{-T}ab^TX^{-T}\]

证明：

这个证明有些复杂。你应该事先了解克罗内克函数和Frobenius内部乘积。对于矩阵X，我们可以写成：

\[\frac{\partial X_{ij}}{\partial X_{kl}} = \delta_{ik}\delta{jl} = \mathcal{H}_{ijkl}\]

你可以将H视为Frobenius内积的标识元素。在开始证明之前，让我们准备好去找逆矩阵的导数。也就是说，∂X^-1/∂X。

\[\begin{align} I^{\prime} &= (XX^{-1})^{\prime} \\ &= X^{\prime}X^{-1} + X(X^{-1})^{\prime} \\ &= 0 \end{align}\]

所以我们可以这么解：

\[X(X^{-1})^{\prime} = -X^{\prime}X^{-1} \rightarrow (X^{-1})^{\prime} = X^{-1}X^{\prime}X^{-1}\]

接着，让我们回到正题：

\[\begin{align} a^TX^{-1}b &= \sum\limits_{i,j=1}^{n,n} a_ib_j(X^{-1})_{ij} \\ &= \sum\limits_{i,j=1}^{n,n} (ab^T)_{ij}(X^{-1})_{ij} \\ &= \sum\limits_{i,j=1}^{n,n} ((ab^T)^T)_{ji}(X^{-1})_{ij} \\ &= tr(ab^T\cdot X^{-1}) \\ &= < ab^T, X^{-1}>_F \end{align}\]

其中F表示Frobenius内积。

接着，带回到原始公式：

\[\begin{align} \frac{\partial a^TX^{-1}b}{\partial X} &= \frac{\partial < ab^T, X^{-1} >_F}{\partial X} \\ &= < ab^T, \frac{\partial X^{-1}}{X} >_F \\ &= < ab^T, \frac{\partial X^{-1}}{X} >_F \\ &= < ab^T, X^{-1}X^{\prime}X^{-1} >_F \\ &= < ab^T, (X^{-T})^T X^{\prime}(X^{-T})^T >_F \\ &= < X^{-T}ab^TX^{-T},X^{\prime} >_F \\ &= < X^{-T}ab^TX^{-T},\mathcal{H} >_F \\ &= X^{-T}ab^TX^{-T} \blacksquare \end{align}\]

现在，我们已经有足够的准备去找到每个参数的梯度了。

对ϕ取导并设为0：

\[\begin{align} \frac{\partial \ell(\phi,\mu_k,\Sigma)}{\partial \phi} &= \sum\limits_{i=1}^m (-0-0+0+\frac{y^i}{\phi}-\frac{1-y^i}{1-\phi})=0\\ &\Rightarrow \sum\limits_{i=1}^m y^i(1-\phi)-(1-y^i)\phi = 0\\ &\Rightarrow \sum\limits_{i=1}^m y^i -m\phi = 0\\ &\Rightarrow \phi = \frac{1}{m}\sum\limits_{i=1}^m \mathbb{1}\{y^{(i)}=1\} \end{align}\]

对 μ_k取导并设为0：

\[\begin{align} \frac{\partial \ell(\phi,\mu_k,\Sigma)}{\partial \mu_k} &= \sum\limits_{i=1}^m (-0-0-\frac{1}{2}2(x_k^i-\mu_k)^T\Sigma^{-1}\mathbb{1}\{y^i=k\})=0\\ &\Rightarrow \sum\limits_{i=1}^m x_k^i\mathbb{1}\{y^i=k\} - \mu_k \mathbb{1}\{y^i=k\} = 0\\ &\Rightarrow \mu_0 = \frac{\sum_{i=1}^m\mathbb{1}\{y^{(i)}=0\}x^{(i)}}{\sum_{i=1}^m\mathbb{1}\{y^{(i)}=0\}}\\ &\Rightarrow \mu_1 = \frac{\sum_{i=1}^m\mathbb{1}\{y^{(i)}=1\}x^{(i)}}{\sum_{i=1}^m\mathbb{1}\{y^{(i)}=1\}} \end{align}\]

对 Σ 取导并设为0:

\[\begin{align} \frac{\partial \ell(\phi,\mu_k,\Sigma)}{\partial \Sigma} &= \sum\limits_{i=1}^m (-\frac{1}{2}\Sigma^{-T}-\frac{1}{2} (\Sigma^{-T}(x_k^i-\mu_k)(x_k^i-\mu_k)^T\Sigma^{-T}))=0\\ &\Rightarrow \sum\limits_{i=1}^m (1-\Sigma^{-T}(x_k^i-\mu_k)(x_k^i-\mu_k)^T) = 0\\ &\Rightarrow m - \sum\limits_{i=1}^m \Sigma^{-T}(x_k^i-\mu_k)(x_k^i-\mu_k)^T = 0\\ &\Rightarrow m\Sigma = \sum\limits_{i=1}^m (x_k^i-\mu_k)(x_k^i-\mu_k)^T\\ &\Rightarrow \Sigma = \frac{1}{m}\sum\limits_{i=1}^m (x^{(i)} - \mu_{y^{(i)}})(x^{(i)} - \mu_{y^{(i)}})^T \end{align}\]

结果如图所示：

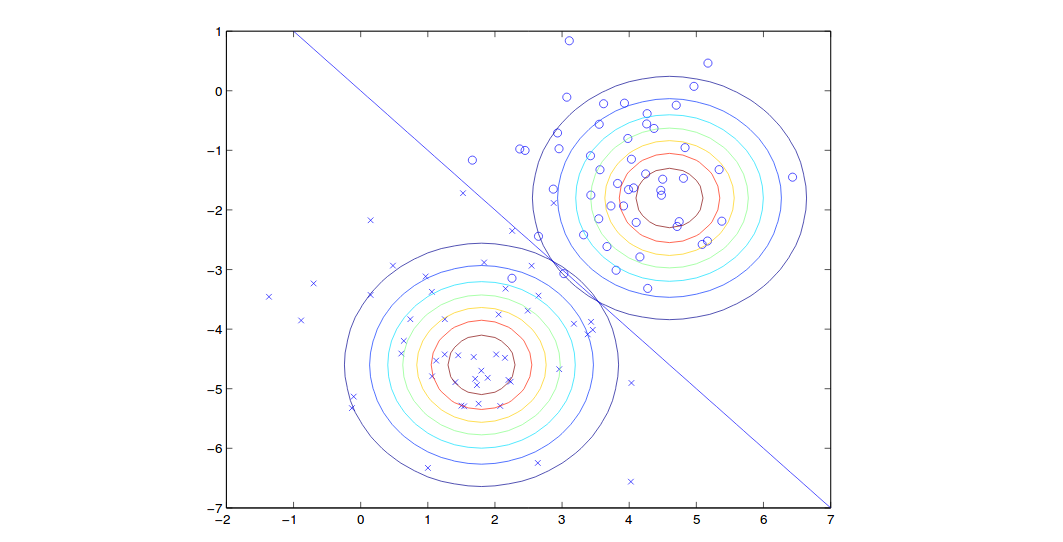
请注意，由于有着同样的协方差，因此上图两个轮廓的形状是相同的，然而均值不同。在边界线这条线上（自左上到右下的直线），每个类的概率为50%。

4.2 高斯判别分析（GDA）和逻辑回归

高斯判别分析又是如何与逻辑回归相关联的呢？我们可以发现如果上述p(x|y) 是具有共同协方差的多元高斯，我们就可以计算p(x|y)并证明它是遵循逻辑函数的。要证明这一点，我们可以：

\[p(y=1\lvert x;\phi,\mu_0,\mu_1,\Sigma) = \frac{p(x,y=1,;\phi,\mu_0,\mu_1,\Sigma)}{p(x;\phi,\mu_0,\mu_1,\Sigma)}\] \[\begin{align} &=\frac{p(y=1\lvert x;\phi)p(x\lvert \mu_1,\Sigma)}{p(y=1\lvert x;\phi)p(x\lvert \mu_1,\Sigma) + p(y=0\lvert x;\phi)p(x\lvert \mu_0,\Sigma)} \\ &= \frac{\phi\mathcal{N}(x\lvert \mu_1,\Sigma)}{\phi\mathcal{N}(x\lvert \mu_1,\Sigma) + (1- \phi)\mathcal{N}(x\lvert \mu_0,\Sigma)} \\ &= \frac{1}{1 + \frac{(1- \phi)\mathcal{N}(x\lvert \mu_0,\Sigma)}{\phi\mathcal{N}(x\lvert \mu_1,\Sigma)}} \\ \end{align}\]

由于高斯属于指数族，我们最终可以将分母中的比率转换为exp（θ^Tx），其中 θ 是φ，μ₀，μ₁，Σ的函数。

同样的，如果p(x|y) 是具有不同 λ 的泊松分布，则p(x|y) 也遵循逻辑函数。 这意味着GDA模型本身有一个强假设，即每个类的数据都可以用具有共享协方差的高斯模型建模。但是，如果这个假设是正确的话，GDA将可以更好并且更快地训练模型。

另一方面，如果不能做出假设，逻辑回归就不那么敏感了。因此，你可以直接使用逻辑回归，而无需接触高斯假设或泊松假设。

5 朴素贝叶斯

在高斯判别分析中，随机变量应使用具有连续值特征的数据。 而朴素贝叶斯则用于学习离散值随机变量，如文本分类。在文本分类中，模型基于文本中的单词将文本标记为二进制类，单词被向量化并用于模型训练。一个单词向量就像一本字典一样，其长度是字典中单词储存的数量，其二进度值则代表着是否为某个词。 一个单词在单词向量中由1表示“存在”，由0表示不存在这个单词。

比方说，一个Email的向量可以表示为：

\[x = \begin{bmatrix} 1 \\ 1 \\ 0 \\ \vdots \\ 1 \\ \vdots \end{bmatrix}\]

其中前两个词可以是“运动”和“篮球” 。（因为原著大佬很喜欢打篮球，所以这里他用了运动和篮球作为例子…）

然而，这可能并不起作用。比方说，如果我们有50000个单词（len(x) = 50000）并尝试将其建模为多项分布。定义上讲，我们可以对$p(x\lvert y)$建模，其中p为多项分布。由于每个单词都只有两个状态，要么存在要么不存在，这就是二元情况。对于多项分布，我们必须对所有可能性进行建模，这意味着类的数量将会是一封邮件中所有可能结果的总和。这种情况下，对于给定的类，每个单词既可以是独立的，也可以是非独立的，这并不要紧。要紧的是我们将其建模为多项分布后，参数的维数将会是$2^{50000}-1$，这实在是太大了。因此，为了解决这个问题，我们做出了朴素贝叶斯假设：

在朴素贝叶斯假设中 - 基于给定分类，每个词彼此之间条件独立。

具体来说，如果我们有一封已被标记为“运动”分类的邮件，则“篮球”一词的出现与“扣篮”一词的出现相互独立。基于以上假设，我们可以独立地对每个单词进行建模，我们可以将它建模为伯努利分布。当然，我们知道这个假设也许是错误的，这也是它之所以被称Naive的原因（Naive是朴素贝叶斯中朴素的英文，它也有天真的、无知的、幼稚的意思）。但根据我的个人经验，朴素贝叶斯将给你提供相当不错的结果。如果你打算删除此假设的话，你需要对数据依赖性进行大量的额外计算。

所以，我们有：

\[\begin{align} P(x_1,...,x_{50000}\lvert y) &=P(x_1\lvert y)P(x_2\lvert y,x_1)\\ &...P(x_{50000}\lvert y,x_1,x_2,...,x_{49999}) \\ &=\prod\limits_{i=1}^{n} P(x_i\lvert y) \end{align}\]

我们对第一步应用概率论中的链式法则，对第二步应用朴素贝叶斯假设。

找到对数似然函数值的最大值：

\[\begin{align} \mathcal{L}(\phi_y,\phi_{j\lvert y=0},\phi_{j\lvert y=1}) &= \prod\limits_{i=1}^{m} P(x^{(i)},y^{(i)}) \\ &=\prod\limits_{i=1}^{m} P(x^{(i)} \lvert y^{(i)}) P(y^{(i)}) \end{align}\]

其中 ϕ _j|y=1 = P(x_j=1|y=1), ϕ_j|y=0 = P(x_j=1|y=0) 并且 ϕ_y= p(y=1)。 这些是我们需要训练的参数。

我们可以对其求导:

\[\begin{align} \phi_{j\lvert y=1} &= \frac{\sum_{i=1}^m \mathbb{1}\{x_j^i = 1 \text{and} y^i = 1\}}{\sum_{i=1}^m \mathbb{1}\{y^i = 1\}} \\ \phi_{j\lvert y=0} &= \frac{\sum_{i=1}^m \mathbb{1}\{x_j^i = 1 \text{and} y^i = 0\}}{\sum_{i=1}^m \mathbb{1}\{y^i = 0\}} \\ \phi_y &= \frac{\sum_{i=1}^m \mathbb{1}\{y^i = 1\}}{m} \\ \end{align}\]

现在来看，由于每个给定的类学习了50000个参数，参数的总数量大约为100000。这已经比以前少太多了。

为了预测新样本，我们可以使用贝叶斯法则来计算P（y = 1 | x）并比较哪个更高。

\[p(y=1\lvert x) = \frac{p(x\lvert y=1)p(y=1)}{p(x)}\] \[=\frac{p(y=1)\prod_{j=1}^n p(x_j\lvert y=1)}{p(y=0)\prod_{j=1}^n p(x_j\lvert y=0) + p(y=1)\prod_{j=1}^n p(x_j\lvert y=1)}\]

延伸: 在这种情况下，因为y是二进制值（0，1），我们将P（x_i | y）建模为伯努利分布。 也就是说，它可以是“有那个词”或“没有那个词”。 伯努利将类标签作为输入并对其概率进行建模，前提是它必须是二进制的。 如果是处理非二进制值X_i，我们可以将其建模为多项式分布，多项式分布可以对多个类进行参数化。

总结: 朴素贝叶斯适用于离散空间，高斯判别分析适用于连续空间。我们任何时候都能将其离散化。

6 拉普拉斯平滑处理

上面的示例通常是好的，不过当新邮件中出现过去训练样本中不存在的单词时，该模型将会预测失败。 在这种情况下，它会因为模型从未看到过这个词而导致两个类的φ变为零，以至于无法进行预测。

这时我们则需要另一个解决方案，其名为拉普拉斯平滑，它将每个参数设置为：

\[\begin{align} \phi_{j\lvert y=1} &= \frac{\sum_{i=1}^m \mathbb{1}\{x_j^i = 1 \text{and} y^i = 1\}+1}{\sum_{i=1}^m \mathbb{1}\{y^i = 1\}+2} \\ \phi_{j\lvert y=0} &= \frac{\sum_{i=1}^m \mathbb{1}\{x_j^i = 1 \text{and} y^i = 0\}+1}{\sum_{i=1}^m \mathbb{1}\{y^i = 0\}+2} \\ \phi_j &= \frac{\sum_{i=1}^{m} \mathbb{1}[z^{(i)}] + 1}{m+k} \\ \end{align}\]

其中k是类的数量。在实际操作中，拉普拉斯平滑并没有太大的区别，因为我们的模型中通常包含了所有的单词。不过有个Plan B总是极好的~