Decision Trees Chinese Version
请注意: 本文是我翻译的一份学习资料,英文原版请点击Wei的学习笔记:Decision Trees 我将不断和原作者的英文笔记同步内容,定期更新和维护。
简介
决策树是当下使用的最流行的非线性框架之一。目前为止,我们学过的支持向量机和广义线性都是线性模型的例子,内核化则是通过映射特征$\phi(x)$得出非线性假设函数。决策树因其对噪声的鲁棒性和学习析取表达式的能力而闻名。实际上,决策树已被广泛运用于贷款申请人的信用风险测评中。
决策树使用二进制规则将输入$x\in \mathbb{R}^d$映射到输出y。从自上而下的角度,树中的每个节点都有一个拆分规则。在最底部,每个叶节点输出一个值或一个类。注意,输出可以重复。每个拆分规则可以表征为:
\[h(x) = \mathbb{1}[x_j > t]\]对于某些维度j和$t\in \mathbb{R}$,我们可以从叶节点了解到预测结果。以下是一个决策树的例子:
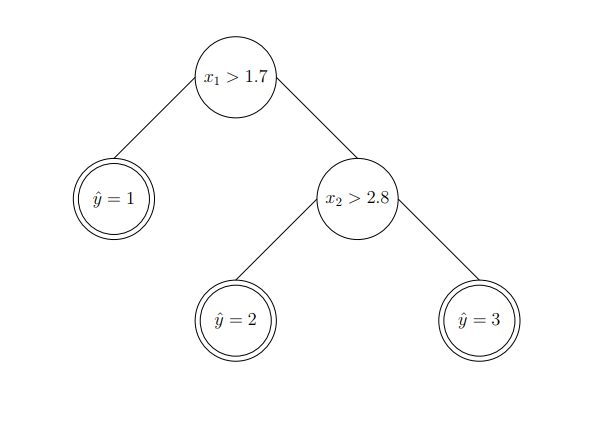
决策树种类
与传统预测模型类似,决策树可以分为分类树和回归树。分类树用于对输入进行分类,而回归树通过回归输出真实数值作为预测结果。
回归树
在这种情况下,决策树的运行就像是对空间进行分割,并以此对结果进行预测。例如,我们有一个二维输入空间,在这个空间内我们可以单独对每个维度进行划分,并为某个区域提供回归值。具体可以参考下图的左侧。
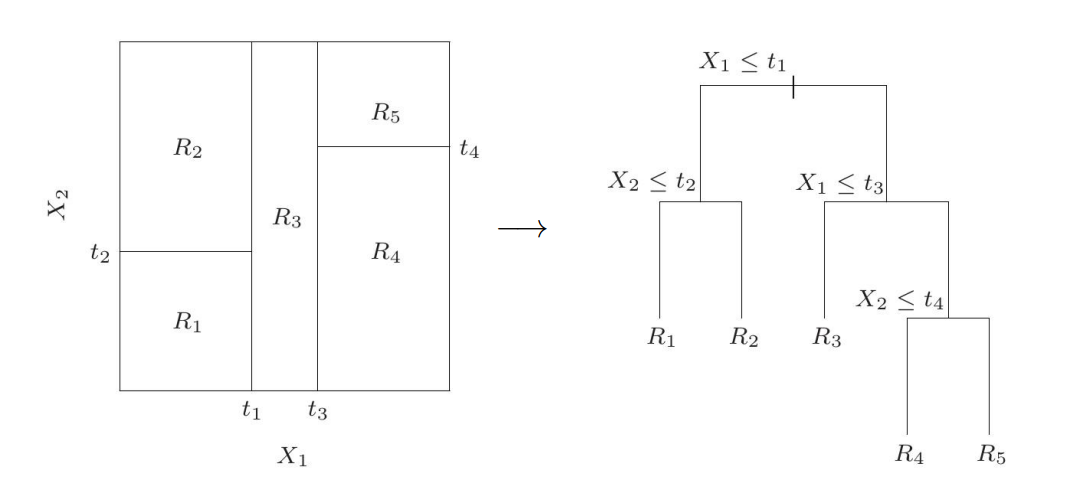
回归树事实上是一个如上图中的右侧的树形结构。为了预测,我们将$R_1,R_2,R_3,R_4,R_5$分配给它们的相应路径。在3D空间中,上面的回归树在3D空间中的分割是阶梯式的,如下图所示。
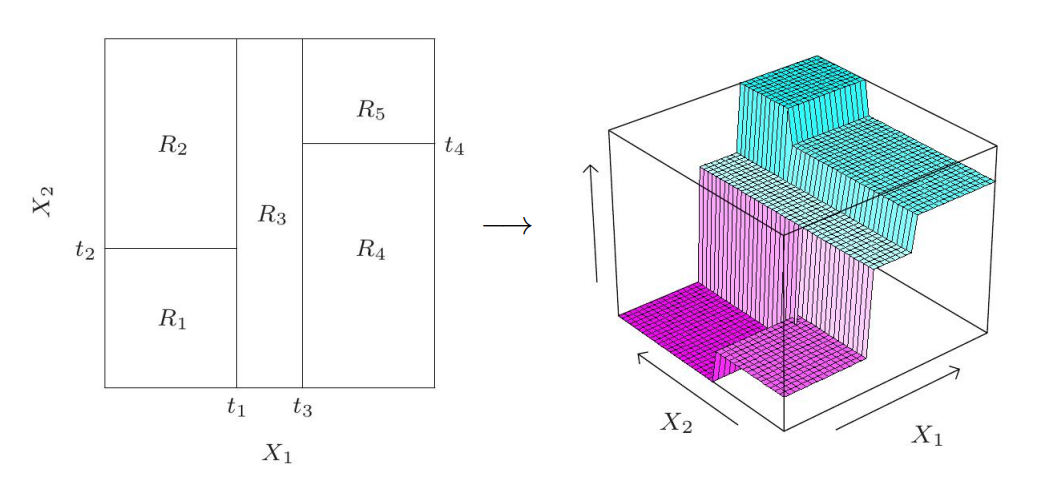
分类树
让我们看一下分类决策树的例子。假设我们有两个特征$x_1,x_2$作为输入,三个类标签作为输出,定义上也就是说$x \in \mathbb{R}^2$ and $y \in {1,2,3}$,在图中我们可以看到:
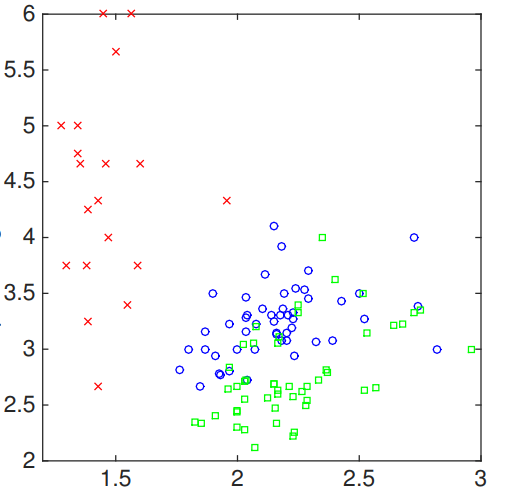
现在,我们可以从第一个特征开始下手。那么我们选择1.7作为要分割的阈值。因此,我们可以:
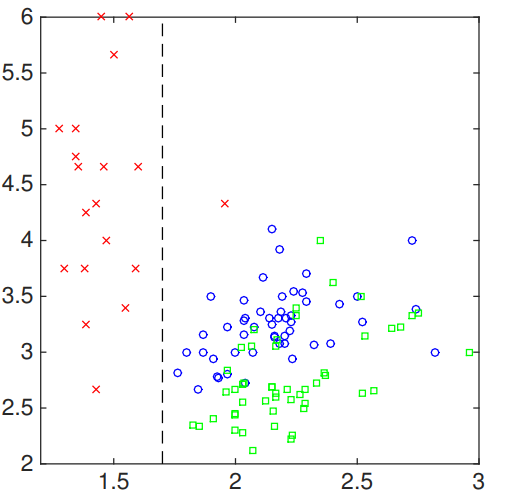
输出的决策树可以描述为:
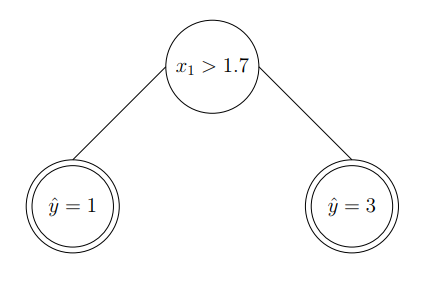
我们可以对输入的第二个特征执行类似的操作。我们在第二特征空间选择另一个阈值,其结果是:
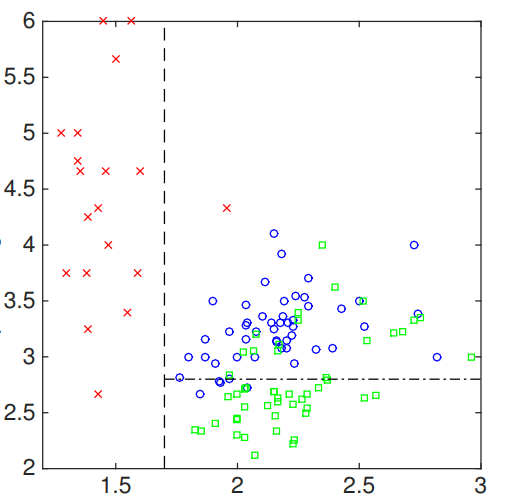
生成的决策树可以显示为:
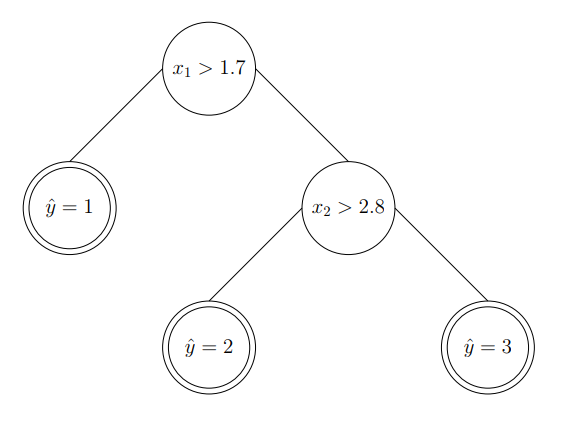
上述步骤显示了从输入空间构建分类决策树的流程。
决策树学习算法
在本节中,我们将讨论这两种类型决策树的学习算法。通常,学习树使用自上而下的贪婪算法。在此算法中,我们从单个节点开始,找出可以最大程度上降低不确定性的阈值。我们重复这一过程,直到找到所有的阈值。
回归树学习算法
回到例子中:

在左图中,我们有五个区域,两个输入特征和四个阈值。让我们推广到M个区域$R_1,\dots,R_M$。那么我们的预测公式可以是:
\[f(x) = \sum\limits_{m=1}^M c_m \mathbb{1} \{x\in R_m \}\]其中$R_m$是x所属的区域,$c_m$是预测值。
目标是尽量减少:
\[\sum\limits_i (y_i - f(x_i))^2\]我们先来看看定义。这里我们有两个变量需要确定,$c_m, R_m$,其中$c_m$为预测结果。那么如果基于给定的$R_m$,我们是否可以更容易地预测$c_m$呢?答案是肯定的。我们可以简单地求出将该区域所有样本的平均值,作为$c_m$。现在的问题是:我们如何找出这些区域?
初始区域通常是整个数据集,首先我们在维度j的阈值s处分割一个区域R。我们可以定义$R^{-}(j,s) = { x_i\in\mathbb{R}^d\lvert x_i(j) \leq s }$ and $R^{+}(j,s) = { x_i\in\mathbb{R}^d\lvert x_i(j) \geq s }$。那么,对于每个维度j,我们计算并找到最佳分裂点s。我们应该为每个现有的区域(叶节点)执行此操作,并根据定义好的度量标准选择出最佳区域分割。
简而言之,我们需要选择一个区域(叶节点),然后选择一个特征,再之后选择一个阈值来形成一个新的分割。
分类树学习算法
在回归树任务中,我们使用了平方误差来确定分割规则的质量。在分类任务中,我们则有更多的选择来评估分割质量。
总的来说,在决策树生长中有三种常见的分类测量方法。
1, 分类误差: $1 - \max_k p_k$
2, 基尼指数: $1 - \sum_k p_k^2$
3, 信息熵:$-\sum_k p_k \ln p_k$
其中$p_k$代表每个类的经验概率(empirical portion),k表示类索引。对于二元分类,如果我们绘制出每次评估相对于$p_k$的值,我们可以看到:
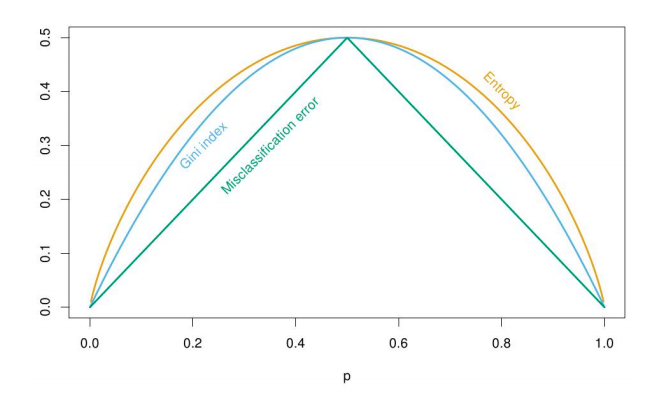
这证明了:
1, 当$p_k$在$R_m$中的K类上是均匀分布时,所有评估都是最大化的
2, 当$p_k = 1$或 0 时,所有评估都被最小化
一般而言,我们希望最大化原始损失与分割区域的基数加权损之差。定义上讲,
\[L(R_p) = \frac{\lvert R_1\rvert L(R_1) + \lvert R_2\lvert L(R_2)}{\lvert R_1\lvert +\lvert R_2\lvert}\]然而,不同的损失函数各有利弊。对于分类误差类型,它的问题是对分割区域的变化不敏感。例如,如果我们组成一个父区域$R_p$,请看下图:
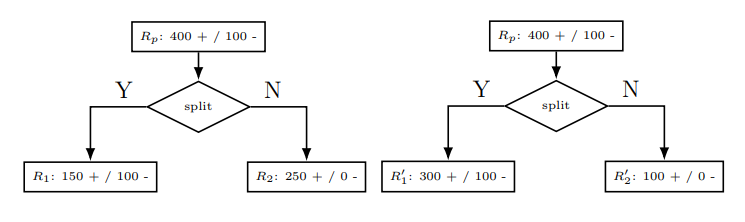
虽然以上两个分割是不同的,不过我们可以发现:
\[L(R_p) = \frac{\lvert R_1\rvert L(R_1) + \lvert R_2\lvert L(R_2)}{\lvert R_1\lvert +\lvert R_2\lvert} = \frac{\lvert R_1^{\prime}\rvert L(R_1^{\prime}) + \lvert R_2^{\prime}\lvert L(R_2^{\prime})}{\lvert R_1^{\prime}\lvert +\lvert R_2^{\prime}\lvert} =100\]我们注意到,如果我们使用分类误差类型,不同的拆分结果也会计算出相同的损失值。此外,我们还看到新的分割区域不会减少原始损失。这是因为,严格上来讲,分类误差损失并非凹函数(concave function)。因此,如果我们绘制上面的分割示例,我们可以看到:
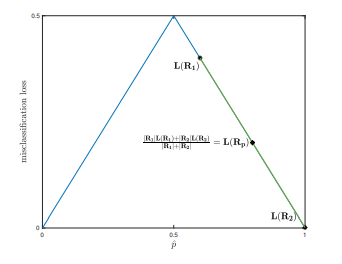
从上图中,我们看出分类误差损失对我们并没有多大的帮助。另一方面,如果我们使用信息熵损失,在图中的显示则与其不同。
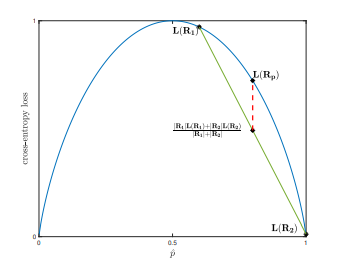
从图中可以看出,我们使用信息熵损失方法分割父区域后,得到的损失将减少。这是因为熵函数是凹函数。
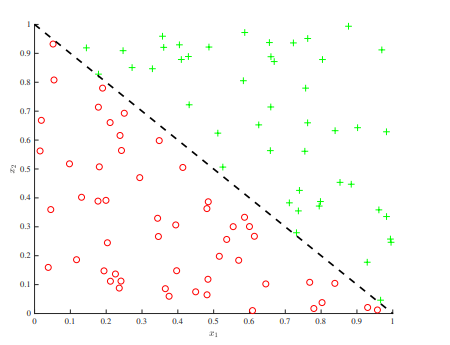
让我们看一个示例,这个示例将使用Gini索引作为损失函数来生成分类树。让我们假设我们有一个2D空间,空间中绘制了一些分类点。图像如下面所示:
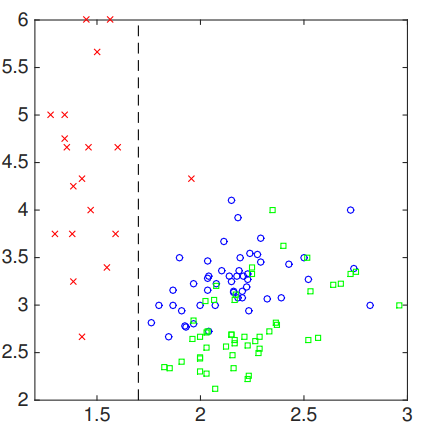
在这种情况下,左边$R_1$区域被分类为标签1。我们可以看到它被近似完美地分类,那么我们可以确定对该区域的测量应该是不错的。
区域2的话,由于基尼指数并不为零,我们需要下更多功夫。如果我们计算基尼指数,我们可以:
\[G(R_2) = 1 - (\frac{1}{101})^2 - (\frac{50}{101})^2 - (\frac{50}{101})^2 = 0.5089\]接下来,我们希望看到不同轴上不同位置的分割点如何根据某些评估函数影响该区域的基尼指数。这样的评估函数,即不确定性函数,可以是:
\[G(R_m) - (p_{r_m^-}G(R_m^-) + p_{r_m^+}G(R_m^+))\]其中$p_{R_m^+}$是$R_m$中的$R_m^+$的占比,$G(R_m^+)$是新区域$R_m^+$的基尼指数。那么,我们希望新的分割区域的基尼指数为零。因此,我们希望最大化原始区域的基尼指数与新区域基尼指数的加权和之差。因此,我们希望将基尼指数上的减少量设为y,不同的分裂点设为x,并绘制出函数。
对于上面的例子,首先我们沿着水平轴来查看不同的分裂点。
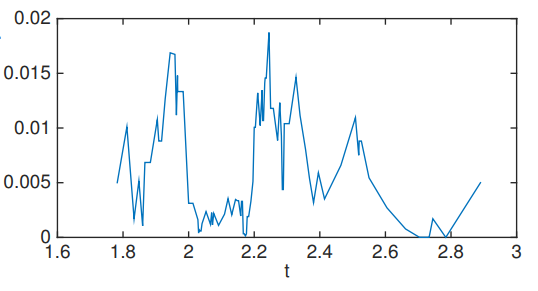
你可以看到图的两侧有两个明显的切口,这是因为小于大约1.7左右的点属于标签1,大约在2.9之后就没有任何点了。我们还可以尝试通过沿另一个轴(即垂直轴)滑动来观察结果。
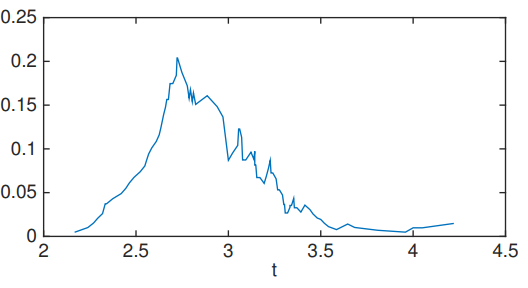
从图中可以看出,垂直分裂点在值为2.7附近有最大的改进。那么,我们可以将数据样本拆分为:
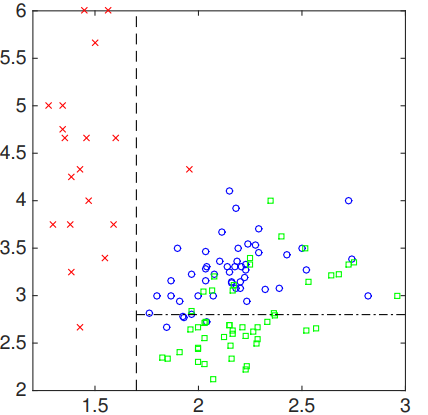
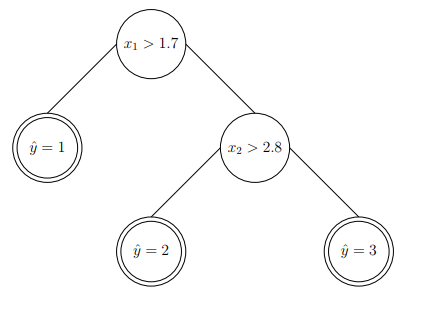
最终的决策树:
正规化
那么问题来了,我们什么时候选择停止决策树的生长呢?当然,你可以说当叶子只包含一种标签时,我们就停止训练。然而,这将导致高方差和低偏差问题,也就是说过度拟合。一些现有的解决方式如下所示:
1,最小叶子结点大小:我们可以设置最小叶子结点大小。
2,最大深度:我们还可以在树深度上设置阈值。
3,最大节点数:当树中的节点数达到叶节点的阈值时,我们可以停止训练。
然而,即便我们可以使用这些方法以避免过度拟合,仍然很难训练一个在一般情况下表现良好的决策树。因此,我们将在另一部分笔记中讲解一种称为集成方法的训练技术。
缺少累加结构
在每个决策树节点的决策阶段,决策规则只能有一个,且规则只能基于某一个特征而制定。这个特征只能从现有的两个特征($x_1$ 或 $x_2$)中选择,而不能用另一个新建的特征。这将会为决策树带来一些问题。如下图所示,我们必须在每个轴上设置多个分裂点以保证准确性,因为每次只允许分割一个特征空间。这就是为什么下图中总是出现平行线的原因。
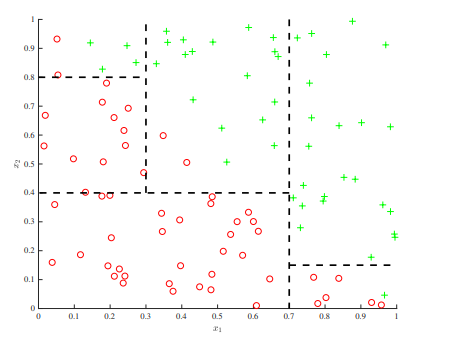
但是,通过累加结构,我们可以很容易地绘制出此图的线性边界。