K-Means

Introduction

In supervised learning, we are always given all the labels/ground truth in training phase. This makes it supervised property. Note that in general that supervised learning assumes that each sample is i.i.d. in the training and testing samples.

In unsupervised learning, we are not given any labels or ground truth for training. We are simply taking input into training model. We call it unsupervised learning.

K-means Clustering Algorithm

K-means clustering algorithm is a standard unsupervised learning algorithm for clustering. K-means will usually generate K clusters based on the distance of data point and cluster mean. On the other hand, knn clustering algorithm usually will return clusters with k samples for each cluster. Keep in mind that there is no label or ground truth required.

We are given a training set ${x^{(1)},x^{(2)},\dots,x^{(m)}}$ where $x^{(i)}\in \mathbb{R}^n$. These are our training samples. The output should be a vector c of cluster assignment for each sample and K mean vectors $\mu$. Formally,

Input: $\mathcal{X}\in \mathbb{R}^n$

Output:

$c=(c_1,c_2,\dots,c_m)$ where $c_i\in{1,\dots,K}$

$\mu=(\mu_1,\mu_2,\dots,\mu_k)$ where $\mu_k\in\mathbb{R}^n$

Then, we need to define an objective function that will give us good c and $\mu$ and is easy to optimize.

An intuitive way is to use Euclidean distance as a measurement. The goal is just to find good centroids with corresponding assignments for each sample. Formally, we want:

\[\mu^{\ast},c^{\ast} = \arg\min_{\mu,c}\sum\limits_{i=1}^m\sum\limits_{k=1}^K \mathbb{1}\{c_i=k\} \lvert\lvert x_i-\mu_k\rvert\rvert^2\]

Thus, our loss function can be defined as:

\[\begin{align} \mathcal{L} &= \sum\limits_{i=1}^m\sum\limits_{k=1}^K \mathbb{1}\{c_i=k\} \lvert\lvert x_i-\mu_k\rvert\rvert^2 \\ &= \sum\limits_{i=1}^m\lvert\lvert x^i - \mu_{c^i}\rvert\rvert^2 \end{align}\]

By looking at this function, we can realize that this is a non-convex function. That means we cannot find the global optimal $\mu$ and c. We can only find a local optimum of them.

Gradient-based optimization

So the frist try is to use gradient-based algorithm to optimize.

Since we cannot take derivative of the loss function w.r.t. c, so we have to use iterative algorithm. Recall:

\[w^{t+1} = w^t - \eta\triangledown_w\mathcal{L}\]

However, it is easily realized that this is hard because:

First, w needs to be continuous-valued. The vector c is not in this case.

Second, it will not go to a better value if step size is too big.

So we seek for an alternative way to this loss function, which is coordinate descent algorithm

Coordinate Descent Algorithm

So the loss function is:

\[\mathcal{L} = \sum\limits_{i=1}^m\sum\limits_{k=1}^K \mathbb{1}\{c_i=k\} \lvert\lvert x_i-\mu_k\rvert\rvert^2\]

Although we cannot find the best $\mu$ and c at the same time, we can:

(1) fix $\mu$, we find the best c exactly.

(2) fix c, we find the best $\mu$ exactly.

The next step is to come up with a formula for updating each parameter.

For updating c:

We rewrite the loss function as:

\[\mathcal{L} = \underbrace{\bigg(\sum\limits_{k=1}^K\mathbb{1}[c_1=k]\lvert\lvert x_1-\mu_k\rvert\rvert^2\bigg)}_{\text{distance of }x_1\text{to its assigned centroid}} + \dots + \underbrace{\bigg(\sum\limits_{k=1}^K\mathbb{1}[c_1=k]\lvert\lvert x_m-\mu_k\rvert\rvert^2\bigg)}_{\text{distance of }x_m\text{to its assigned centroid}}\]

We can minimize this function w.r.t. each $c_i$ by minimizing each term above individually. This solution is:

\[c^i = \arg\min_j\lvert\lvert x^i - \mu_j\rvert\rvert^2\]

Because c is discrete, there is no derivative. We simply calculate all the possible values for $c_i$ and pick the smallest.

For updating $\mu$:

This time, we rewrite the loss function as:

\[\mathcal{L} = \underbrace{\bigg(\sum\limits_{i=1}^m\mathbb{1}[c_i=1]\lvert\lvert x_i-\mu_1\rvert\rvert^2\bigg)}_{sum squared distance of data in cluster 1} + \dots + \underbrace{\bigg(\sum\limits_{i=1}^m\mathbb{1}[c_i=K]\lvert\lvert x_i-\mu_K\rvert\rvert^2\bigg)}_{sum squared distance of data in cluster K}\]

For each k, let $n_k = \sum_{i=1}^m\mathbb{1}[c_i=k]$. Then,

\[\mu_k = \arg\min_{\mu}\sum\limits_{i=1}^m\mathbb{1}[c_i=k]\lvert\lvert x_i-\mu_k\rvert\rvert^2\] \[\mu_k = \frac{1}{n_k} \sum\limits_{i=1}^m x_i\mathbb{1}[c_i=k]\]

Then we can formally define K-means clustering algorithm as:

1 Initialize cluster centroids $\mu_1,\mu_2,\dots,\mu_k\in \mathbb{R}^n$ randomly

2 Repeat until convergence:

     For every i, set $c^i = \arg\min_j\lvert\lvert x^i - \mu_j\rvert\rvert^2$

     For each j, set $\mu_j = \frac{\sum_{i=1}^m\mathbb{1}[c^i=j]x^i}{\sum_{i=1}^m\mathbb{1}[c^i=j]}$

Intuitively, we can think it this way: given a particular $\mu$, we are able to find the best c but once c is changed we can probably find a better $\mu$. We do this in a cycled way to optimize loss function.

K is the parameter that we need to pre-define. This is called parametric laerning. After selecting K, we can ramdomly pick up K samples to be our K centroids. Surly, we can use some other way to initialize them.

The figure of learning process can show this process.

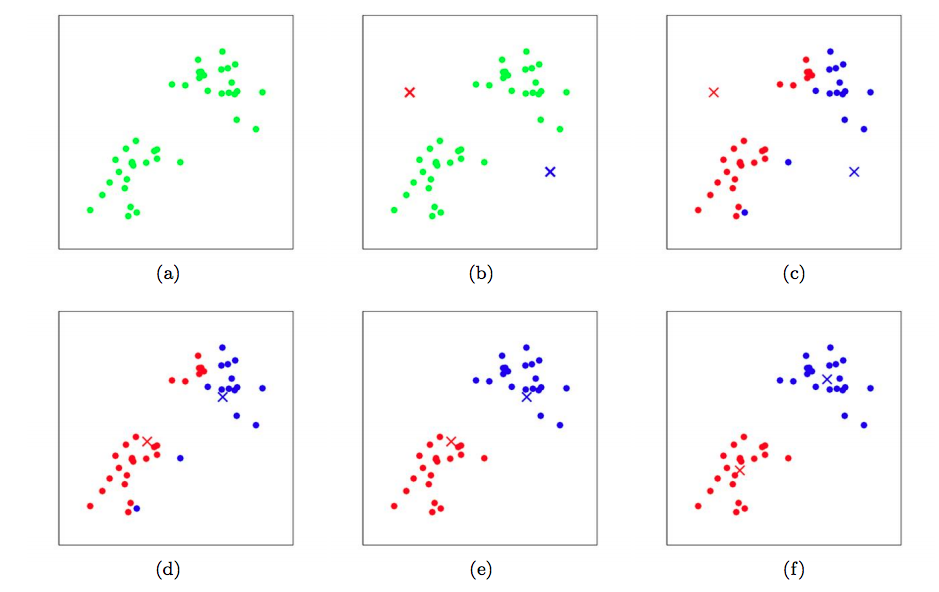
Plot (a) is the plot of samples. Plot (b) is samples with centroids. The rest plots show the training process.

A natural question to ask is: Is the k-means algorithm guaranteed to converge?

The answer is yes.

We have shown that k-means algorithm is exactly coordinate descent on $\mathcal{L}$. Remember that coordinate descent is to minimize the cost function with respect to one of the variables while holding the others static. Every update to c and $\mu$ decreases the loss function to the previous value. Thus, we can always find out that $\mathcal{L}$, c and $\mu$ will always converge.

Since J is non-convex function, coordinate descent is not guaranteed to converge to the global minimum. Rather, it will always converge to local mimimum. Intuitively, we can see that when c stops changing, the algorithm has converged to a local ooptimal solution. There might be other solutions of c where we can get the same loss function and even better. This is the reault of not being convex.

To avoid this, we can run k-means several times with different initilizations and choose the best in terms of J.

How to select K

Recall that K-means is a parameteric learning algorithm. That means we need to manually set up a K for the algorithm to work. So how do we select a good K?

The K-means objective function decreases as K increases. This is no magic. Some simple methods to choose K are that:

1 Using advanced information, if you split a set of things among K people, you know K.

2 Looking at the relative decrease in loss function. If $K^{\ast}$ is the best, then increasing K when $K<K^{\ast}$ should decrease $\mathcal{L}$ much more than when $K>K^{\ast}$.

3 Seeking for non-parameteric learning. I will talk about that later.